頂点シェーダーで登場する座標変換
管理人は現在、Mechtatelというゲームエンジンを開発しています。
(まだゲームエンジンと呼べるようなクオリティではないですが…)
この記事で解説するのは頂点シェーダ(vertex shader)で行っている以下のような処理についてです。
(たとえば、Mechtatelの標準シェーダーであるalbedo.vertを参照のこと)
gl_Position=camera.proj*camera.view*pc.model*vec4(inPosition,1.0);Mechtatelは現在のところVulkanを利用していますが、OpenGLやDirectXであっても、シェーダもしくはアプリケーション側で同じような処理を行うことになるのではないかと思います。
簡単のため、上のコードの処理を数式で表現しておきます。
$$ \boldsymbol{p}_{\rm{clip}}=M_{\rm{proj}}M_{\rm{view}}M_{\rm{model}}\boldsymbol{p}_{\rm{local}} $$
この式は、オブジェクトのローカル座標$\boldsymbol{p}_{\rm{local}}$をクリップ空間座標$\boldsymbol{p}_{\rm{clip}}$に変換する処理を表しています。
この記事では、それぞれの座標と変換行列について一つずつ説明していきたいと思います。
ローカル座標
ローカル座標(local coordinates)は、そのオブジェクトが所属するローカル空間における座標です。
少し語弊があるかもしれませんが、たとえばある部屋に複数の人がいて、それぞれの人が自分自身を中心とする座標系をもっているとき、それがローカル座標です。
AさんにはAさんを中心とした座標系があり、Bさんも同様です。
部屋の中に存在するそれぞれの人についてローカル座標が存在します。
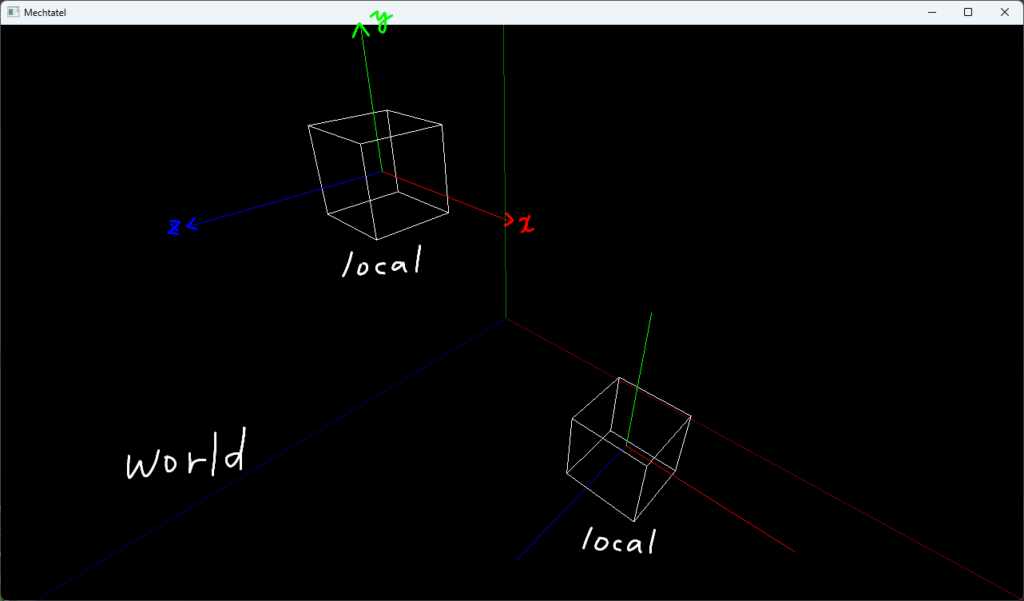
Mechtatelでは、オブジェクトの中心が常に原点に存在するようなローカル座標系を想定しているので、オブジェクト中心のローカル座標$\boldsymbol{p}_{\rm{local}}$は
$$ \boldsymbol{p}_{\rm{local}}= \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} $$
で、平行移動や回転によって変化しません。
ここで「オブジェクトの中心」と言っているのは、各頂点の平均を計算しているわけではなく、あくまでオブジェクトが作成されたときの中心点がローカル座標の原点にあるとみなしている、ということです。
詳しくはわかりませんが、ここの実装はゲームエンジンによって異なるかもしれません。
ところで、3次元の座標に次元を一つ追加した
$$ \boldsymbol{p}= \begin{pmatrix} x \\ y \\ z \\ w \end{pmatrix} $$
という形式の座標を同次座標(homogeneous coordinates)と呼びます。
同次座標を用いると平行移動や回転を行列で表現するのに便利なため、この形式を用いるのが一般的です。
$w=1$のときは位置を表し、$w=0$のときは方向を表します。
ワールド空間座標
ワールド空間座標(world-space coordinates)はその世界全体での座標です。
たとえば部屋の中心を原点とする座標系で、それぞれの人が部屋のどこにいるのか(各ローカル座標系の位置)を表すことができます。
自分中心だった座標系を、部屋を中心とした座標系に変換します。
ワールド空間座標を$\boldsymbol{p}_{\rm{world}}$とすると、$\boldsymbol{p}_{\rm{world}}=M_{\rm{model}}\boldsymbol{p}_{\rm{local}}$で表せます。 $M_{\rm{model}}$がモデル行列(model matrix)と呼ばれ、ローカル座標をワールド空間座標に変換する役割をもちます。
ローカル座標とワールド空間座標がともに直交座標系なら、平行移動と拡大・縮小は以下の行列で表現できます。
空白になっている成分は0です。
$$ \begin{gather*} M_{\rm{translate}}= \begin{pmatrix} 1 & & & x \\ & 1 & & y \\ & & 1 & z \\ & & & 1 \end{pmatrix} \\ M_{\rm{scaling}}= \begin{pmatrix} x & & & \\ & y & & \\ & & z & \\ & & & 1 \end{pmatrix} \end{gather*} $$
回転は少し複雑になりますが、たとえば$x$軸回りに角度$\theta$だけ回転する行列は、
$$ M_{\rm{rotx}}= \begin{pmatrix} 1 & & & \\ & \cos\theta & -\sin\theta & \\ & \sin\theta & \cos\theta & \\ & & & 1 \end{pmatrix} $$
これらを組み合わせることで、ローカル座標からワールド空間座標への変換を行うモデル行列を作ります。
たとえば、$(x,y,z)=(1,2,3)$平行移動してから$x$軸回りに$\frac{\pi}{2}$回転する場合は、
$$ \begin{align*} M_{\rm{model}}&=M_{\rm{rotx}}M_{\rm{translate}} \\ &= \begin{pmatrix} 1 & & & \\ & \cos\frac{\pi}{2} & -\sin\frac{\pi}{2} & \\ & \sin\frac{\pi}{2} & \cos\frac{\pi}{2} & \\ & & & 1 \end{pmatrix} \begin{pmatrix} 1 & & & 1 \\ & 1 & & 2 \\ & & 1 & 3 \\ & & & 1 \end{pmatrix} \end{align*} $$
ローカル座標が直交座標系でない場合(極座標など)は、モデル行列で直交座標系に変換します。
(ワールド座標以降の座標系は直交座標系を用いるのが一般的かと思います)
ビュー空間座標
The engine don’t move the ship at all.
The ship stays where it is and the engines move the universe around it.
(エンジンは船を全く動かさない。船はその場にとどまり、エンジンが船のまわりの世界を動かすのだ)
─Futurama
ここでカメラという概念が登場します。
現実世界であれば見たい方向にカメラを動かしますが、3Dグラフィックスの世界ではカメラは固定してあり、代わりにそのまわりの世界をカメラの画角に収まるように動かします。
たとえば、カメラは常にワールド空間の原点にあり、$y$軸の正の方向を上として$z$軸の正の方向を向いているとします。
このカメラの画角に収まるように、部屋の中にいる人を平行移動および回転させる必要があります。
このような座標変換を行う行列$M_{\rm{view}}$をビュー行列(view matrix)と呼び、ビュー行列によって変換された座標をビュー空間座標(view-space coordinates)と呼びます。
ビュー空間座標を$\boldsymbol{p}_{\rm{view}}$とすると、$\boldsymbol{p}_{\rm{view}}=M_{\rm{view}}\boldsymbol{p}_{\rm{world}}$となります。
この変換を行うためには、仮想的なカメラのワールド空間での
- 位置$\boldsymbol{p}_{\rm{eye}}$
- 視線の方向$\boldsymbol{v}_{\rm{target}}$
- カメラの上方向$\boldsymbol{v}_{\rm{up}}$
が必要となります。
カメラの上方向がわからないとロール($z$軸回りの回転)が定まらないので、上方向の情報も必要になります。
カメラを横に傾けると映像も傾くことを想定してもらえればいいと思います。
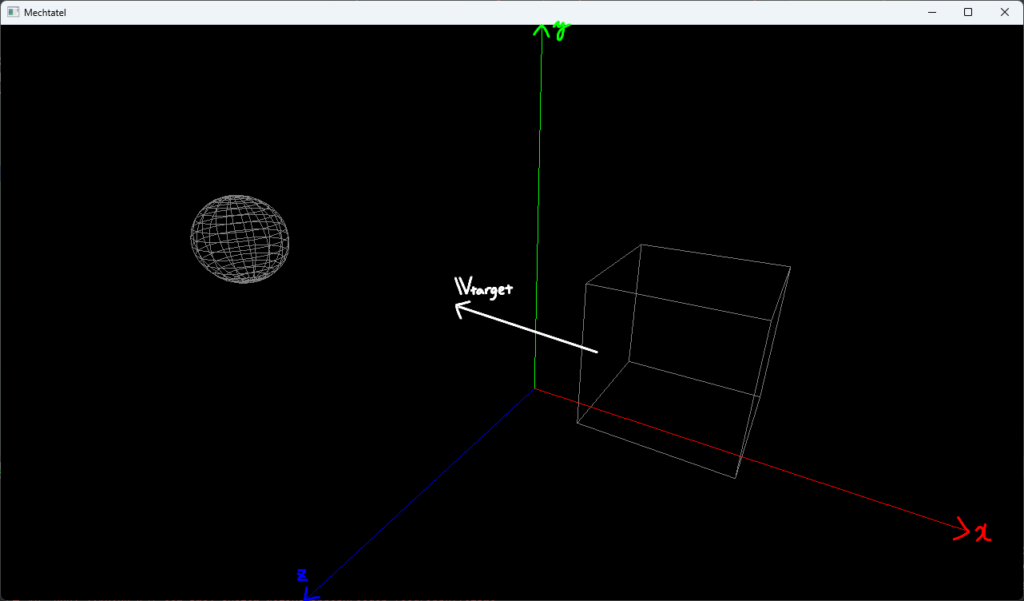
ここで、$\boldsymbol{p}_{\rm{eye}}=(x_e\space y_e\space z_e)^{\rm{T}}$とします。
まずはカメラを原点まで平行移動します。
平行移動を行う行列$T$は、
$$ T= \begin{pmatrix} 1 & & & -x_e \\ & 1 & & -y_e \\ & & 1 & -z_e \\ & & & 1 \end{pmatrix} $$
となります。
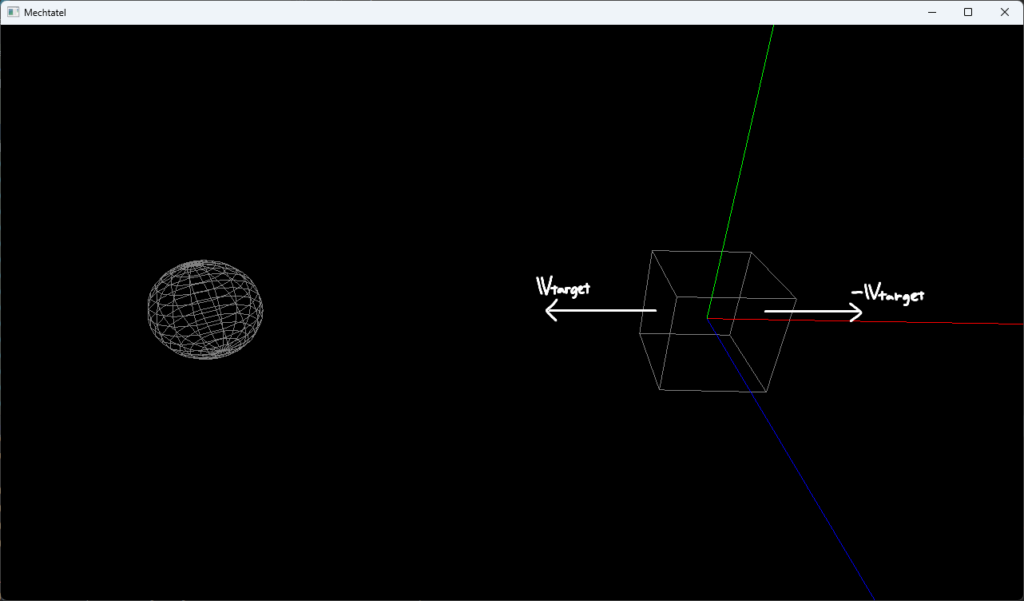
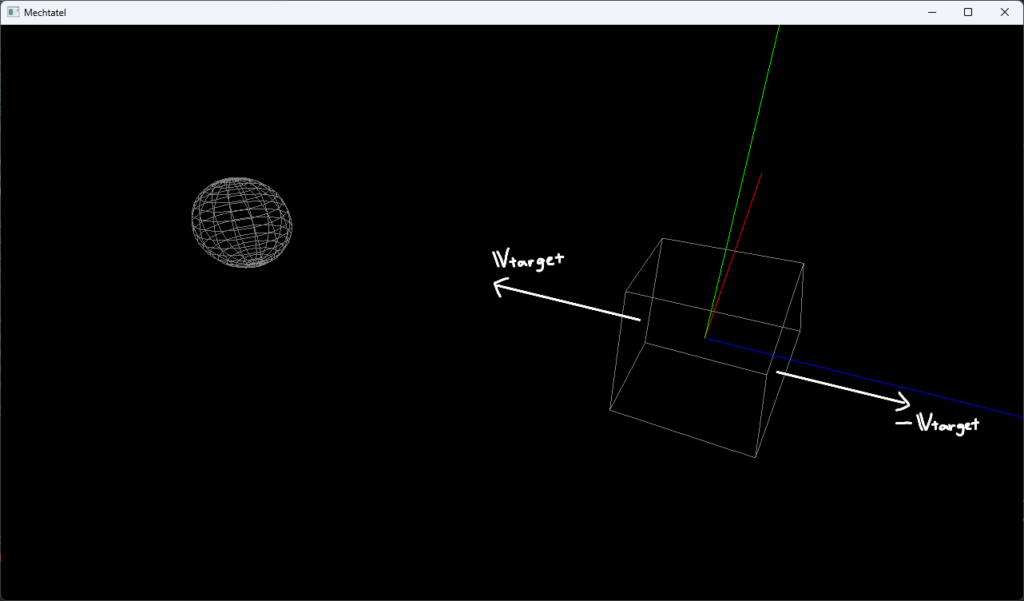
ここで、カメラを基準とした正規直交基底を求めます。
視線の方向$\boldsymbol{v}_{\rm{target}}$が$z$軸の正の方向としたいので、$z$軸方向の基底は$\boldsymbol{e}’_z=-\boldsymbol{v}_{\rm{target}}/|\boldsymbol{v}_{\rm{target}}|=(x_z\space y_z\space z_z)^{\rm{T}}$とします。
視線の逆ベクトルを基底としているのは、座標系を右手系にしておきたいからです。
このままだと視線の逆方向を基準にした座標系になってしまいますが、この後のクリップ空間座標を求めるときに$z$軸を反転することで修正します。
さらに、
$$ \begin{align*} \boldsymbol{e}’_x&=\frac{\boldsymbol{v}_{\rm{up}}\times \boldsymbol{e}’_z}{|\boldsymbol{v}_{\rm{up}}\times \boldsymbol{e}’_z|}=(x_x\space y_x\space z_x)^{\rm{T}} \\ \boldsymbol{e}’_y&=\boldsymbol{e}’_z\times\boldsymbol{e}’_x=(x_y\space y_y\space z_y)^{\rm{T}} \end{align*} $$
とすれば、三つの基底がそろいます。
$\boldsymbol{v}_{\rm{up}}=(x_u\space y_u\space z_u)^{\rm{T}}$として$\boldsymbol{e}’_x$の具体的な成分を計算すると、
$$ \left\{ \begin{align*} x_x&=y_uz_z-z_uy_z \\ y_x&=z_ux_z-x_uz_z \\ z_x&=x_uy_z-y_ux_z \end{align*} \right. $$
となります。
$\boldsymbol{e}’_y$を計算すると、
$$ \left\{ \begin{align*} x_y&=y_z(x_uy_z-y_ux_z)-z_z(z_ux_z-x_uz_z) \\ y_y&=z_z(y_uz_z-z_uy_z)-x_z(x_uy_z-y_ux_z) \\ z_y&=x_z(z_ux_z-x_uz_z)-y_z(y_uz_z-z_uy_z) \end{align*} \right. $$
となります。
ここでの目標は、
$$ \begin{gather*} \boldsymbol{e}’_x \to \boldsymbol{e}_x=(1\space 0\space 0)^{\rm{T}} \\ \boldsymbol{e}’_y \to \boldsymbol{e}_y=(0\space 1\space 0)^{\rm{T}} \\ \boldsymbol{e}’_z \to \boldsymbol{e}_z=(0\space 0\space 1)^{\rm{T}} \\ \end{gather*} $$
となるような変換を求めることです。
この変換を行う行列を$R$とおくと、
$$ \left\{ \begin{align*} &\boldsymbol{e}_x=R\boldsymbol{e}’_x \\ &\boldsymbol{e}_y=R\boldsymbol{e}’_y \\ &\boldsymbol{e}_z=R\boldsymbol{e}’_z \end{align*} \right. $$
を満たす$R$を求めればいいことになります。
この$R$を直接求めようとしましたがどうも計算がうまくいかないので、まずは$\boldsymbol{e}’_x=P\boldsymbol{e}_x$を満たすような$P$を求めて、それから$R=P^{-1}$の関係を用いて$R$を求めたいと思います。
$P$の各要素を以下のように表現することにします。
$$ P= \begin{pmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \\ \end{pmatrix} $$
$\boldsymbol{e}’_x=P\boldsymbol{e}_x$より、
$$ \begin{pmatrix} x_x \\ y_x \\ z_x \\ 0 \end{pmatrix} = \begin{pmatrix} m_{00} & & & \\ & \ddots & & \\ & & \ddots & \\ & & & m_{33} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} m_{00} \\ m_{10} \\ m_{20} \\ m_{30} \end{pmatrix} $$
なので、
$$ \left\{ \begin{align*} &m_{00}=x_x \\ &m_{10}=y_x \\ &m_{20}=z_x \\ &m_{30}=0 \end{align*} \right. $$
$\boldsymbol{e}’_y=P\boldsymbol{e}_y$と$\boldsymbol{e}’_z=P\boldsymbol{e}_z$についても同様の計算で、それぞれ
$$ \left\{ \begin{align*} &m_{01}=x_y\\ &m_{11}=y_y \\ &m_{21}=z_y \\ &m_{31}=0 \end{align*} \right. $$
$$ \left\{ \begin{align*} &m_{02}=x_z \\ &m_{12}=y_z \\ &m_{22}=z_z \\ &m_{32}=0 \end{align*} \right. $$
という関係式が得られます。
正規直交基底どうしの変換は回転なので、平行移動を表す成分である$m_{03}=m_{13}=m_{23}=0$となります。
また、位置を表す同次座標($w=1$)を変換した後にも$w=1$になっていてほしいので、$m_{33}=1$となります。
したがって、
$$ P= \begin{pmatrix} x_x & x_y & x_z & 0 \\ y_x & y_y & y_z & 0 \\ z_x & z_y & z_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$
となります。
次に、$P$の逆行列を求めます。
余因子行列を用いる方法で逆行列を求めてみます。
(計算が複雑ですが…)
まず、$P$の行列式$|P|$を求めます。
列の余因子展開を用いると、
$$ \begin{align*} |P|&=m_{00} \begin{vmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{vmatrix} -m_{10} \begin{vmatrix} m_{01} & m_{02} & m_{03} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{vmatrix} \\ &\qquad+m_{20} \begin{vmatrix} m_{01} & m_{02} & m_{03} \\ m_{11} & m_{12} & m_{13} \\ m_{31} & m_{32} & m_{33} \end{vmatrix} -m_{30} \begin{vmatrix} m_{01} & m_{02} & m_{03} \\ m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \end{vmatrix} \\ &=x_x(y_yz_z-y_zz_y)-y_x(x_yz_z-x_zz_y)+z_x(x_yy_z-x_zy_y) \\ &=x_y(y_zz_x-y_xz_z)+y_y(x_xz_z-x_zz_x)+z_y(x_zy_x-x_xy_z) \\ &=x_y\{y_z(x_uy_z-y_ux_z)-(z_ux_z-x_uz_z)z_z\} \\ &\qquad+y_y\{(y_uz_z-z_uy_z)z_z-x_z(x_uy_z-y_ux_z)\} \\ &\qquad+z_y\{x_z(z_ux_z-x_uz_z)-(y_uz_z-z_uy_z)y_z\} \\ &=x_y^2+y_y^2+z_y^2 \end{align*} $$
ここで、$|\boldsymbol{e}’_y|=\sqrt{x_y^2+y_y^2+z_y^2}=1$なので、結果としては、
$$ |P|=1 $$
となります。
次に、行列$P$から$i$行と$j$列を取り除いた小行列を$M_{ij}$とすると、
$$ \begin{align*} &M_{00}= \begin{pmatrix} y_y & y_z & 0 \\ z_y & z_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{01}= \begin{pmatrix} y_x & y_z & 0 \\ z_x & z_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &M_{02}= \begin{pmatrix} y_x & y_y & 0 \\ z_x & z_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{03}= \begin{pmatrix} y_x & y_y & y_z \\ z_x & z_y & z_z \\ 0 & 0 & 0 \end{pmatrix} \\ &M_{10}= \begin{pmatrix} x_y & x_z & 0 \\ z_y & z_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{11}= \begin{pmatrix} x_x & x_z & 0 \\ z_x & z_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &M_{12}= \begin{pmatrix} x_x & x_y & 0 \\ z_x & z_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{13}= \begin{pmatrix} x_x & x_y & x_z \\ z_x & z_y & z_z \\ 0 & 0 & 0 \end{pmatrix} \\ &M_{20}= \begin{pmatrix} x_y & x_z & 0 \\ y_y & y_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{21}= \begin{pmatrix} x_x & x_z & 0 \\ y_x & y_z & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &M_{22}= \begin{pmatrix} x_x & x_y & 0 \\ y_x & y_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{23}= \begin{pmatrix} x_x & x_y & x_z \\ y_x & y_y & y_z \\ 0 & 0 & 0 \end{pmatrix} \\ &M_{30}= \begin{pmatrix} x_y & x_z & 0 \\ y_y & y_z & 0 \\ z_y & z_z & 0 \end{pmatrix} \qquad M_{31}= \begin{pmatrix} x_x & x_z & 0 \\ y_x & y_z & 0 \\ z_x & z_z & 0 \end{pmatrix} \\ &M_{32}= \begin{pmatrix} x_x & x_y & 0 \\ y_x & y_y & 0 \\ z_x & z_y & 0 \end{pmatrix} \qquad M_{33}= \begin{pmatrix} x_x & x_y & x_z \\ y_x & y_y & y_z \\ z_x & z_y & z_z \end{pmatrix} \\ \end{align*} $$
$M_{ij}$の行列式は、
$$ \begin{align*} |M_{00}|&=y_yz_z-y_zz_y \\ |M_{01}|&=z_zy_x-y_zz_x \\ |M_{02}|&=z_yy_x-y_yz_x \\ |M_{03}|&=0 \\ |M_{10}|&=x_yz_z-x_zz_y \\ |M_{11}|&=z_zx_x-x_zz_x \\ |M_{12}|&=z_yx_x-x_yz_x \\ |M_{13}|&=0 \\ |M_{20}|&=x_yy_z-x_zy_y \\ |M_{21}|&=y_zx_x-x_zy_x \\ |M_{22}|&=y_yx_x-x_yy_x \\ |M_{23}|&=0 \\ |M_{30}|&=0 \\ |M_{31}|&=0 \\ |M_{32}|&=0 \\ |M_{33}|&=x_xy_yz_z+x_yy_zz_x+x_zy_xz_y-x_zy_yz_x-y_zz_yx_x-z_zx_yy_x \\ \end{align*} $$
余因子行列$\tilde{P}$の各成分は
$$ \tilde{P}_{ij}=(-1)^{i+j}|M_{ji}| $$
なので、
$$ \begin{align*} \tilde{P}_{00}&=|M_{00}|=y_yz_z-y_zz_y \\ \tilde{P}_{01}&=-|M_{10}|=x_zz_y-x_yz_z \\ \tilde{P}_{02}&=|M_{20}|=x_yy_z-x_zy_y \\ \tilde{P}_{03}&=-|M_{30}|=0 \\ \tilde{P}_{10}&=-|M_{01}|=y_zz_x-z_zy_x \\ \tilde{P}_{11}&=|M_{11}|=x_zx_x-x_zz_x \\ \tilde{P}_{12}&=-|M_{21}|=x_zy_x-y_zx_x \\ \tilde{P}_{13}&=|M_{31}|=0 \\ \tilde{P}_{20}&=|M_{02}|=z_yy_x-y_yz_x \\ \tilde{P}_{21}&=-|M_{12}|=x_yz_x-z_yx_x \\ \tilde{P}_{22}&=|M_{22}|=y_yx_x-x_yy_x \\ \tilde{P}_{23}&=-|M_{32}|=0 \\ \tilde{P}_{30}&=|M_{03}|=0 \\ \tilde{P}_{31}&=-|M_{13}|=0 \\ \tilde{P}_{32}&=|M_{23}|=0 \\ \tilde{P}_{33}&=-|M_{33}|=x_zy_yz_x+y_zz_yx_x+z_zx_yy_x-x_xy_yz_z-x_yy_zz_x-x_zy_xz_y \\ \end{align*} $$
$\tilde{P}_{33}$はもう少し簡単にできそうです。 $\tilde{P}_{33}=1$にならないとおかしいということを念頭に置いて式変形をしてみると、
$$ \begin{align*} &\quad x_zy_yz_x+y_zz_yx_x+z_zx_yy_x-x_xy_yz_z-x_yy_zz_x-x_zy_xz_y \\ &=x_y(y_xz_z-y_zz_x)+y_y(x_zz_x-x_xz_z)+z_y(x_xy_z-x_zy_x) \\ &=x_y^2+y_y^2+z_z^2 \\ &=1 \end{align*} $$
したがって、
$$ \begin{align*} P^{-1}&=\frac{1}{|P|}\tilde{P} \\ &= \begin{pmatrix} y_yz_z-y_zz_y & x_zz_y-x_yz_z & x_yy_z-x_zy_y & 0 \\ y_zz_x-z_zy_x & x_zx_x-x_zz_x & x_zy_x-y_zx_x & 0 \\ z_yy_x-y_yz_x & x_yz_x-z_yx_x & y_yx_x-x_yy_x & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{align*} $$
となります。
これで正規直交基底の変換を行う行列$R=P^{-1}$がわかりました。
最終的なビュー行列は平行移動→回転の順番で座標変換を行えばいいので、
$$ \begin{align*} M_{\rm{view}}&=RT \\ &= \begin{pmatrix} y_yz_z-y_zz_y & x_zz_y-x_yz_z & x_yy_z-x_zy_y & 0 \\ y_zz_x-z_zy_x & x_zx_x-x_zz_x & x_zy_x-y_zx_x & 0 \\ z_yy_x-y_yz_x & x_yz_x-z_yx_x & y_yx_x-x_yy_x & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{align*} $$
ここで求めたビュー行列が正しいか検算してみます。
MechtatelではJOMLというライブラリを採用しています。
JOMLではMatrix4f.lookAtというメソッドを使うことでビュー行列を作成できます。
lookAtメソッドで得られるビュー行列と手動で作成したビュー行列が一致することを確認したいと思います。
public static void main(String[] args) {
var cameraEye = new Vector3f(10.0f, 10.0f, 10.0f);
var cameraCenter = new Vector3f(0.0f, 0.0f, 0.0f);
var cameraUp = new Vector3f(0.0f, 1.0f, 0.0f).normalize();
var cameraTarget = new Vector3f(cameraCenter).sub(cameraEye).normalize();
//ビュー行列を手動で作成する
var ez = new Vector3f(cameraTarget).mul(-1.0f);
var ex = new Vector3f(cameraUp).cross(ez).normalize();
var ey = new Vector3f(ez).cross(ex);
var rMat = new Matrix4f().identity();
rMat.m00(ey.y * ez.z - ez.y * ey.z);
rMat.m10(ez.x * ey.z - ey.x * ez.z);
rMat.m20(ey.x * ez.y - ez.x * ey.y);
rMat.m01(ez.y * ex.z - ez.z * ex.y);
rMat.m11(ez.x * ex.x - ez.x * ex.z);
rMat.m21(ez.x * ex.y - ez.y * ex.x);
rMat.m02(ey.z * ex.y - ey.y * ex.z);
rMat.m12(ey.x * ex.z - ey.z * ex.x);
rMat.m22(ey.y * ex.x - ey.x * ex.y);
var tMat = new Matrix4f().identity();
tMat.m30(-cameraEye.x);
tMat.m31(-cameraEye.y);
tMat.m32(-cameraEye.z);
var viewMat = new Matrix4f(rMat).mul(tMat);
System.out.println("Manually created view matrix is:");
System.out.println(viewMat);
//JOMLのlookAtメソッドを使用する
//lookAtメソッドではカメラの視線ではなく、
//視線を向けている先の位置(center)を指定する
var viewMat2 = new Matrix4f().lookAt(cameraEye, cameraCenter, cameraUp);
System.out.println("View matrix by lookAt method is:");
System.out.println(viewMat2);
}出力結果は以下のようになり、結果が一致することがわかります。
Manually created view matrix is:
7.071E-1 0.000E+0 -7.071E-1 0.000E+0
-4.082E-1 8.165E-1 -4.082E-1 0.000E+0
5.774E-1 5.774E-1 5.774E-1 -1.732E+1
0.000E+0 0.000E+0 0.000E+0 1.000E+0
View matrix by lookAt method is:
7.071E-1 0.000E+0 -7.071E-1 -0.000E+0
-4.082E-1 8.165E-1 -4.082E-1 -0.000E+0
5.774E-1 5.774E-1 5.774E-1 -1.732E+1
0.000E+0 0.000E+0 0.000E+0 1.000E+0クリップ空間座標
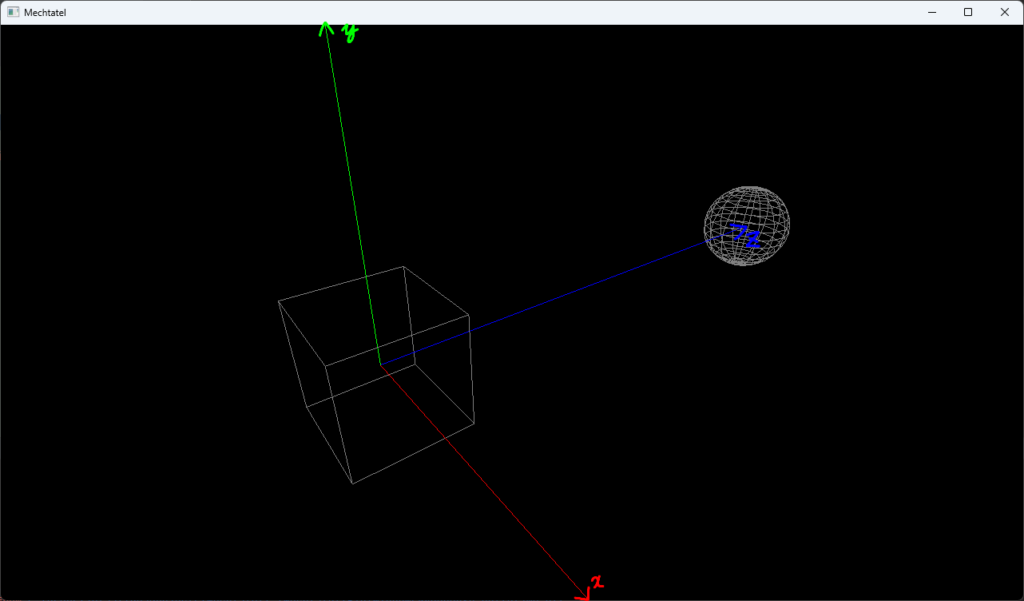
ビュー行列を用いた変換で、原点に固定されたカメラから見た景色を表すビュー空間座標を得ることができました。
いよいよgl_Positionに値をセットする、というところですが、OpenGLやVulkanではgl_Positionの取りうる値の範囲が決まっており、この範囲から外れている頂点はクリップ(破棄)されます。
gl_PositionのxとyについてはOpenGLとVulkan共通で、
-gl_Position.w <= x,y <= gl_Position.wという範囲の値を取ることができます。
カメラは原点にあって$z$軸正の方向を向いているので、$z$はカメラからの距離を表す値になります。gl_Position.zの取りうる範囲はOpenGLとVulkanで異なっており、OpenGLの場合は
-gl_Position.w <= z <= gl_Position.wとなりxやyと同じ範囲ですが、Vulkanの場合は
0 <= z <= gl_Position.wとなり、zが負の値になっているときにはクリップされます。
以上のように、gl_Positionの取りうる値の範囲が決まっているため、ビュー空間座標を変換し、これらの範囲に収まる値にする必要があります。
このような変換を行う行列を射影行列(projection matrix)といい、射影行列によって変換された後の座標をクリップ空間座標(clip-space coordinates)と呼びます。
つまり、gl_Positionには頂点のクリップ空間座標をセットすることになります。
一般的な射影行列としては、平行射影(orthographic projection)と透視射影(perspective projection)の二つがあります。
この二つについて、それぞれ説明していきたいと思います。
平行射影
$xy$平面、$yz$平面、$xz$平面それぞれに平行な面をもつ直方体を考えます。
この直方体の中にある頂点が最終的に描画されるようにしたいです。
これを平行射影(orthographic projection)と呼びます。

ここで、カメラに近い方の面までの距離を$z_{\rm{near}}$、遠い方の面までの距離を$z_{\rm{far}}$とします。
また、カメラの正面にある面の$x$軸正の方向の$x$座標を$x_{\rm{right}}$、負の方向の$x$座標を$x_{\rm{left}}$とし、直方体の上側と下側の$y$座標をそれぞれ$y_{\rm{top}}$、$y_{\rm{bottom}}$とします。
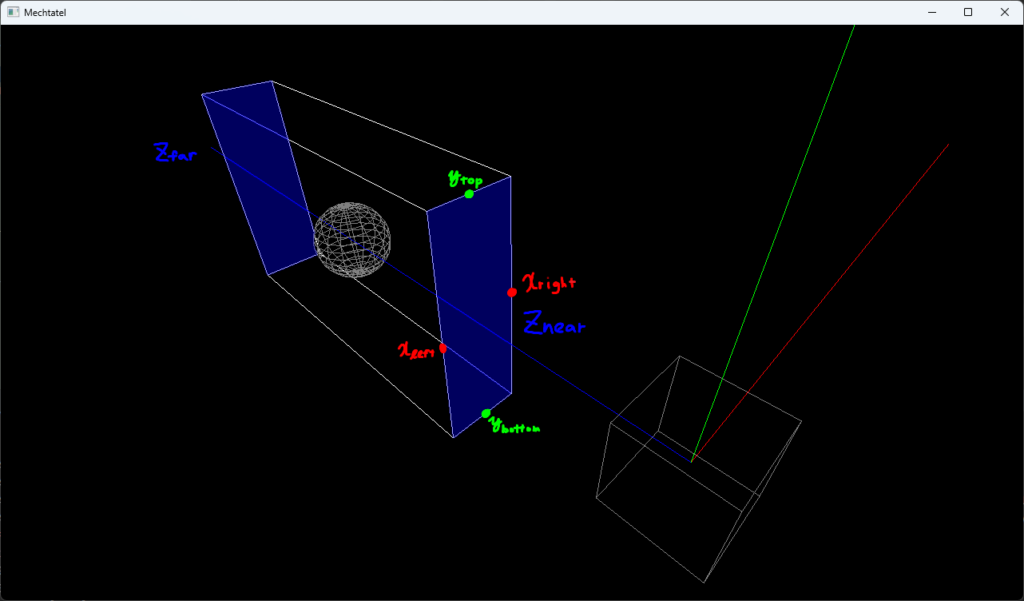
まず、直方体を平行移動します。
OpenGLの場合は直方体の中心が原点に来るようにすればいいので、平行移動を行う行列を$T$とすると、
$$ T= \begin{pmatrix} 1 & & & -\frac{x_{\rm{right}}+x_{\rm{left}}}{2} \\ & 1 & & -\frac{y_{\rm{top}}+y_{\rm{bottom}}}{2} \\ & & 1 & -\frac{z_{\rm{far}}+z_{\rm{near}}}{2} \\ & & & 1 \end{pmatrix} $$
Vulkanの場合は$z_{\rm{near}}$の面が$z=0$に来ればいいので、
$$ T= \begin{pmatrix} 1 & & & -\frac{x_{\rm{right}}+x_{\rm{left}}}{2} \\ & 1 & & -\frac{y_{\rm{top}}+y_{\rm{bottom}}}{2} \\ & & 1 & -z_{\rm{near}} \\ & & & 1 \end{pmatrix} $$
次に、拡大・縮小を行って、直方体がクリップ空間全体を占めるようにします。
OpenGLの場合はクリップ空間の一辺の長さが2なので、直方体をこれに合わせて拡大・縮小します。
(注: 平行射影の場合は普通gl_Position.w = 1とするので、クリップ空間の一辺の長さは1 – (-1) = 2となります)
拡大・縮小を行う行列を$S$とすると、
$$ S= \begin{pmatrix} \frac{2}{x_{\rm{right}}-x_{\rm{left}}} & & & \\ & \frac{2}{y_{\rm{top}}-y_{\rm{bottom}}} & & \\ & & \frac{2}{z_{\rm{far}}-z_{\rm{near}}} & \\ & & & 1 \end{pmatrix} $$
Vulkanの場合は$z$方向の長さは1なので、
$$ S= \begin{pmatrix} \frac{2}{x_{\rm{right}}-x_{\rm{left}}} & & & \\ & \frac{2}{y_{\rm{top}}-y_{\rm{bottom}}} & & \\ & & \frac{1}{z_{\rm{far}}-z_{\rm{near}}} & \\ & & & 1 \end{pmatrix} $$
となります。
まとめると、射影行列$M_{\rm{proj}}=ST$となります。
と言いたいところですが、上の式をそのまま実装すると、JOMLの出力結果と一致しません。
具体的には$z$成分の拡大・縮小を行う部分の符号が反転しているのです。
これが何を意味しているかと言えば、これまで右手系を前提にしていましたが、クリップ空間座標はどうやら左手系にする必要がありそうだ、ということです。
(自分も今まで深く考えたことがありませんでした)
これに関して具体的なドキュメントは見つけられなかったのですが、Stack Overflowなどの回答を参考にすると、OpenGLのクリップ空間座標とその後のNDC (Normalized Device Coordinates; 正規化デバイス座標)は左手系のようです。
そもそもOpenGLで右手系を使うのはただの慣習らしく、確かによく考えてみれば、すべて左手系を使うように実装することもできそうです。
(Vulkanのクリップ空間座標とNDCは右手系ですが、これについては後述)
右手系から左手系への変換は、$z$成分を反転する行列$S_{\rm{LH}}$を使えば実現できます。
$$ S_{\rm{LH}}= \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & -1 & \\ & & & 1 \end{pmatrix} $$
したがって、最終的な射影行列$M_{\rm{proj}}$は、$M_{\rm{proj}}=STS_{\rm{LH}}$となります。
まず世界を左手系に変換してから、先に示した平行移動と拡大・縮小を行います。
この射影行列が正しいかどうか検算してみます。
JOMLではMatrix4f.orthoメソッドを使用することで平行射影を行う行列を作成できます。
public static void main(String[] args) {
float right = 10.0f;
float left = -10.0f;
float top = 10.0f;
float bottom = -10.0f;
float near = 1.0f;
float far = 20.0f;
//手動で射影行列を作成する
var tMat = new Matrix4f().translate(
-(right + left) / 2.0f,
-(top + bottom) / 2.0f,
-(far + near) / 2.0f
);
var tMatVk = new Matrix4f().translate(
-(right + left) / 2.0f,
-(top + bottom) / 2.0f,
-near
);
var sMat = new Matrix4f().scale(
2.0f / (right - left),
2.0f / (top - bottom),
2.0f / (far - near)
);
var sMatVk = new Matrix4f().scale(
2.0f / (right - left),
2.0f / (top - bottom),
1.0f / (far - near)
);
var sLHMat = new Matrix4f().scale(1.0f, 1.0f, -1.0f);
var projMat = new Matrix4f(sMat).mul(tMat).mul(sLHMat);
var projMatVk = new Matrix4f(sMatVk).mul(tMatVk).mul(sLHMat);
System.out.println("Manually created projection matrices are:");
System.out.println("[OpenGL]");
System.out.println(projMat);
System.out.println("[Vulkan]");
System.out.println(projMatVk);
//JOMLのorthoメソッドを利用して射影行列を作成する
var projMat2 = new Matrix4f().ortho(left, right, bottom, top, near, far);
var projMatVk2 = new Matrix4f().ortho(left, right, bottom, top, near, far, true);
System.out.println("Projection matrices created by ortho method are:");
System.out.println("[OpenGL]");
System.out.println(projMat2);
System.out.println("[Vulkan]");
System.out.println(projMatVk2);
}出力結果は以下のようになります。
Manually created projection matrices are:
[OpenGL]
1.000E-1 0.000E+0 0.000E+0 0.000E+0
0.000E+0 1.000E-1 0.000E+0 0.000E+0
0.000E+0 0.000E+0 -1.053E-1 -1.105E+0
0.000E+0 0.000E+0 0.000E+0 1.000E+0
[Vulkan]
1.000E-1 0.000E+0 0.000E+0 0.000E+0
0.000E+0 1.000E-1 0.000E+0 0.000E+0
0.000E+0 0.000E+0 -5.263E-2 -5.263E-2
0.000E+0 0.000E+0 0.000E+0 1.000E+0
Projection matrices created by ortho method are:
[OpenGL]
1.000E-1 0.000E+0 0.000E+0 -0.000E+0
0.000E+0 1.000E-1 0.000E+0 -0.000E+0
0.000E+0 0.000E+0 -1.053E-1 -1.105E+0
0.000E+0 0.000E+0 0.000E+0 1.000E+0
[Vulkan]
1.000E-1 0.000E+0 0.000E+0 -0.000E+0
0.000E+0 1.000E-1 0.000E+0 -0.000E+0
0.000E+0 0.000E+0 -5.263E-2 -5.263E-2
0.000E+0 0.000E+0 0.000E+0 1.000E+0透視射影
透視射影(perspective projection)では錐台(frustum)の中にある頂点が描画されることになります。
近くのものほど大きく、遠くのものほど小さく見える遠近法の効果が追加されます。

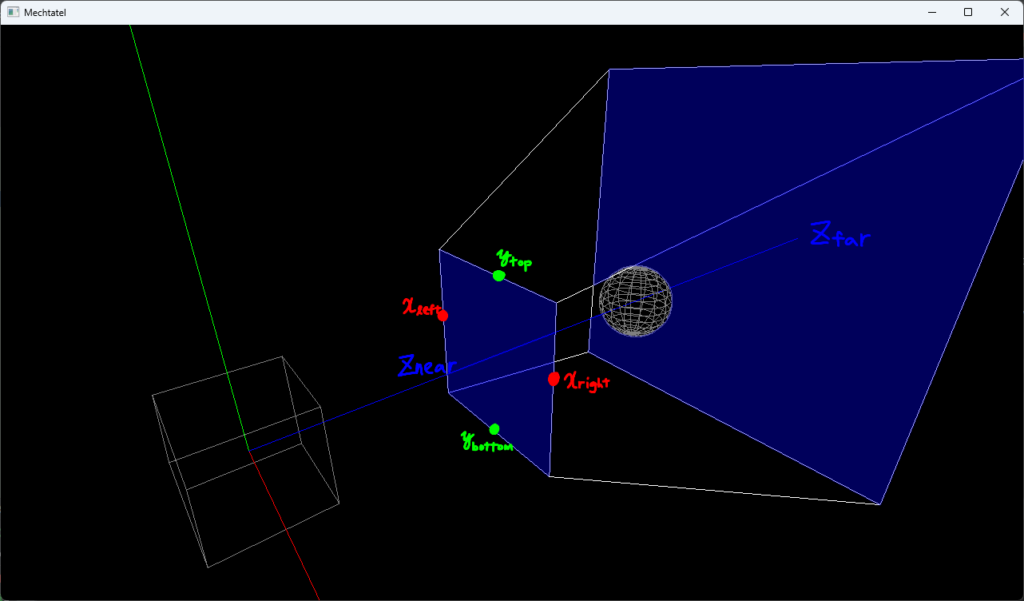
この空間に点$\boldsymbol{p}=(x_p\space y_p\space z_p)^{\rm{T}}$があるとします。
この点を$z_{\rm{near}}$の面に射影したとき、その座標$\boldsymbol{s}=(x_s\space y_s\space z_s)^{\rm{T}}$は、
$$ \left\{ \begin{align*} x_s&=\frac{x_p}{z_p}z_{\rm{near}} \\ y_s&=\frac{y_p}{z_p}z_{\rm{near}} \end{align*} \right. $$
となります。
これは単純に一次関数と$z_{\rm{near}}$面との交点を求めているだけです。
$x_s$は$x_{\rm{left}}\leq x_s\leq x_{\rm{right}}$、$y_s$は$y_{\rm{bottom}}\leq y_s\leq y_{\rm{top}}$の範囲にあるので、これを$[-1,1]$の範囲になるようにスケーリングします。
スケーリング後の座標を$\boldsymbol{s}’=(x_s’\space y_s’\space z_s’)^{\rm{T}}$とすると、
$$ \left\{ \begin{align*} x_s’&=2\cdot\frac{x_s-x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}}-1 \\ y_s’&=2\cdot\frac{y_s-y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}}-1 \end{align*} \right. $$
これに先の式を代入して整理すると、
$$ \left\{ \begin{align*} x_s’&=\frac{2z_{\rm{near}}}{x_{\rm{right}}-x_{\rm{left}}}\cdot\frac{x_p}{z_p}-\frac{x_{\rm{right}}+x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}} \\ y_s’&=\frac{2z_{\rm{near}}}{y_{\rm{top}}-y_{\rm{bottom}}}\cdot\frac{y_p}{z_p}-\frac{y_{\rm{top}}+y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}} \end{align*} \right. $$
$z_s’$については、$\frac{1}{z_p}$に比例する値を取ると考え、
$$ z_s’=\frac{A}{z_p}+B $$
と表します。
このように考える理由ですが、$z_p$が$z_{\rm{near}}$に近いとき(カメラの近くにある頂点の場合)は、どの頂点がカメラのより近くにあるのかを高い精度で判別したいのに対し、$z_p$が$z_{\rm{far}}$に近いとき(カメラから遠くにある頂点の場合)は、それほど精度が求められないことが多いためです。
たとえば、目の前の机にある積み木を描画するときには、どの積み木がよりカメラの近くにあるかという情報が重要なのに対し、はるか遠くの入道雲を描画するときには、普通どの雲が一番カメラに近いかといった情報は重要ではなく、ざっくりとした精度で前後を判別できれば問題ありません。
具体的なグラフで表せば、$z_p$と$z_s’$の関係は以下のようにしたいです。
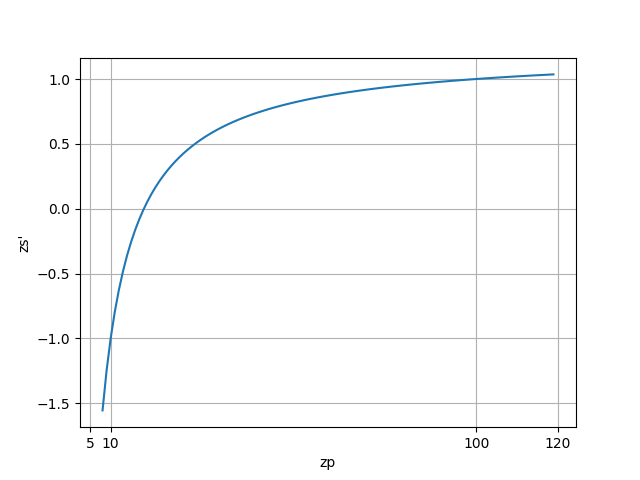
このグラフでは、$z_{\rm{near}}=10$、$z_{\rm{far}}=100$としています。
$z_p$が$z_{\rm{near}}$に近いときは$z_p$の微小な変化でも$z_s’$が大きく変化し、逆に$z_p$が$z_{\rm{far}}$に近いときは多少$z_p$が変化しても$z_s’$は少ししか変化しません。
$z_p=z_{\rm{near}}$のとき$z_s’=-1$、$z_p=z_{\rm{far}}$のとき$z_s’=1$となるように先の式の$A$と$B$を決めます。
$A$と$B$が満たす条件は、
$$ \left\{ \begin{align*} -1&=\frac{A}{z_{\rm{near}}}+B \\ 1&=\frac{A}{z_{\rm{far}}}+B \end{align*} \right. $$
この方程式を解くと、
$$ \left\{ \begin{align*} A&=-2\cdot\frac{z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} \\ B&=\frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} \end{align*} \right. $$
となります。
したがって、$z_s’$は、
$$ z_s’=-\frac{2z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}}\cdot\frac{1}{z_p}+\frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} $$
となります。
まとめると、
$$ \left\{ \begin{align*} x_s’&=\frac{2z_{\rm{near}}}{x_{\rm{right}}-x_{\rm{left}}}\cdot\frac{x_p}{z_p}-\frac{x_{\rm{right}}+x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}} \\ y_s’&=\frac{2z_{\rm{near}}}{y_{\rm{top}}-y_{\rm{bottom}}}\cdot\frac{y_p}{z_p}-\frac{y_{\rm{top}}+y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}} \\ z_s’&=-\frac{2z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}}\cdot\frac{1}{z_p}+\frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} \end{align*} \right. $$
これを行列の形にしたいですが、$\frac{1}{z_p}$だと都合が悪いので、両辺に$z_p$をかけます。
$$ \left\{ \begin{align*} x_s’z_p&=\frac{2z_{\rm{near}}}{x_{\rm{right}}-x_{\rm{left}}}\cdot x_p-\frac{x_{\rm{right}}+x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}}\cdot z_p \\ y_s’z_p&=\frac{2z_{\rm{near}}}{y_{\rm{top}}-y_{\rm{bottom}}}\cdot y_p-\frac{y_{\rm{top}}+y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}}\cdot z_p \\ z_s’z_p&=-\frac{2z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}}+\frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}}\cdot z_p \end{align*} \right. $$
この計算を行列の形にすると、
$$ \begin{pmatrix} \frac{2z_{\rm{near}}}{x_{\rm{right}}-x_{\rm{left}}} & 0 & -\frac{x_{\rm{right}}+x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}} & 0 \\ 0 & \frac{2z_{\rm{near}}}{y_{\rm{top}}-y_{\rm{bottom}}} & -\frac{y_{\rm{top}}+y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}} & 0 \\ 0 & 0 & \frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} & -\frac{2z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x_p \\ y_p \\ z_p \\ 1 \end{pmatrix} $$
となります。
注目してほしいのは座標変換を行った後の同次座標の$w$成分です。
変換後の$w$成分には$z_p$の値がそのままセットされます。
$x_s’, y_s’, z_s’$は$[-1,1]$の範囲を取るので、それに$z_p$をかけた値は$[-z_p,z_p]$の範囲を取ることになります。
この範囲は頂点によって異なりますが、重要なのは、$z_p$で割れば$[-1,1]$の範囲になるということです。
クリップ空間座標は頂点ごとに異なる$[-z_p,z_p]$の値を取りますが、この後のNDCでは$[-1,1]$の範囲に収める必要があります。
そのため、クリップ空間座標の$w$成分に$z_p$の値を保持しておき、後の処理で使えるようにします。
以上より、最終的な射影行列$M_{\rm{proj}}$は、$M_{\rm{proj}}=M_{\rm{perspective}}S_{\rm{LH}}$となります。
$$ \begin{align*} M_{\rm{proj}}&=M_{\rm{perspective}}S_{\rm{LH}} \\ &= \begin{pmatrix} \frac{2z_{\rm{near}}}{x_{\rm{right}}-x_{\rm{left}}} & 0 & -\frac{x_{\rm{right}}+x_{\rm{left}}}{x_{\rm{right}}-x_{\rm{left}}} & 0 \\ 0 & \frac{2z_{\rm{near}}}{y_{\rm{top}}-y_{\rm{bottom}}} & -\frac{y_{\rm{top}}+y_{\rm{bottom}}}{y_{\rm{top}}-y_{\rm{bottom}}} & 0 \\ 0 & 0 & \frac{z_{\rm{far}}+z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} & -\frac{2z_{\rm{far}}z_{\rm{near}}}{z_{\rm{far}}-z_{\rm{near}}} \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & & & \\ & 1 & & \\ & & -1 & \\ & & & 1 \end{pmatrix} \end{align*} $$
ところで、$x_{\rm{left}},x_{\rm{right}},y_{\rm{bottom}},y_{\rm{top}}$はカメラのアスペクト(画角の幅と高さの比率)と$x$方向または$y$方向のFOV (Field of View; 画角の角度)の二つの情報があれば計算することができます。
$y$方向のFOVを$\theta_y$とすると、$y_{\rm{bottom}}$と$y_{\rm{top}}$はそれぞれ、
$$ \left\{ \begin{align*} y_{\rm{bottom}}&=-z_{\rm{near}}\tan\frac{\theta_y}{2} \\ y_{\rm{top}}&=z_{\rm{near}}\tan\frac{\theta_y}{2} \end{align*} \right. $$
カメラのアスペクトを$r$とすると、$r$は
$$ r=\frac{x_{\rm{right}}-x_{\rm{left}}}{y_{\rm{top}}-y_{\rm{bottom}}} $$
で、これを用いると、
$$ x_{\rm{right}}-x_{\rm{left}}=r(y_{\rm{top}}-y_{\rm{bottom}}) $$
なので、
$$ \left\{ \begin{align*} x_{\rm{left}}&=-\frac{1}{2}r(y_{\rm{top}}-y_{\rm{bottom}}) \\ x_{\rm{right}}&=\frac{1}{2}r(y_{\rm{top}}-y_{\rm{bottom}}) \end{align*} \right. $$
となります。
ここで求めた射影行列が正しいかどうか検算してみます。
JOMLではMatrix4f.perspectiveメソッドを使用することで透視射影を行う行列を作成できます。
今回はOpenGL用の射影行列のみ作成します。
public static void main(String[] args) {
float aspect = 1.0f;
float fovY = (float) Math.toRadians(60.0f);
float zNear = 1.0f;
float zFar = 100.0f;
//手動で射影行列を作成する
float yTop = zNear * (float) Math.tan(fovY / 2.0f);
float yBottom = -yTop;
float xRight = aspect * (yTop - yBottom) / 2.0f;
float xLeft = -xRight;
var persMat = new Matrix4f().zero();
persMat.m00(2.0f * zNear / (xRight - xLeft));
persMat.m20(-(xRight + xLeft) / (xRight - xLeft));
persMat.m11(2.0f * zNear / (yTop - yBottom));
persMat.m21(-(yTop + yBottom) / (yTop - yBottom));
persMat.m22((zFar + zNear) / (zFar - zNear));
persMat.m32(-2.0f * zFar * zNear / (zFar - zNear));
persMat.m23(1.0f);
var sLHMat = new Matrix4f().scale(1.0f, 1.0f, -1.0f);
var projMat = new Matrix4f(persMat).mul(sLHMat);
System.out.println("Manually created projection matrix is:");
System.out.println(projMat);
//JOMLのperspectiveメソッドを使用して射影行列を作成する
var projMat2 = new Matrix4f().perspective(fovY, aspect, zNear, zFar);
System.out.println("Projection matrix created by perspective method is:");
System.out.println(projMat2);
}出力結果は以下のようになります。
Manually created projection matrix is:
1.732E+0 0.000E+0 0.000E+0 0.000E+0
0.000E+0 1.732E+0 0.000E+0 0.000E+0
0.000E+0 0.000E+0 -1.020E+0 -2.020E+0
0.000E+0 0.000E+0 -1.000E+0 0.000E+0
Projection matrix created by perspective method is:
1.732E+0 0.000E+0 0.000E+0 0.000E+0
0.000E+0 1.732E+0 0.000E+0 0.000E+0
0.000E+0 0.000E+0 -1.020E+0 -2.020E+0
0.000E+0 0.000E+0 -1.000E+0 0.000E+0透視射影を行う場合の注意点
透視射影を行う場合、$z_{\rm{near}}$は可能な限り大きく、$z_{\rm{far}}$は可能な限り小さく設定するのが基本です。
先に示したとおり、透視射影では$z$が$z_{\rm{near}}$に近いときは高い精度で前後を判別できますが、$z_{\rm{far}}$に近づくにつれて精度が荒くなります。
ゲームをプレイしていて、遠くのオブジェクトがちらつくという現象に遭遇したことがある方もいると思いますが、これは似たような距離にある複数のオブジェクトの前後を正しく判定できないことによって生じる現象で、Z-fightingと呼ばれます。
$z_{\rm{far}}/z_{\rm{near}}$の値が極端に大きいとZ-fightingが起こりやすいため、注意する必要があります。
Vulkanにおける射影行列
OpenGLではクリップ空間座標とその後のNDCは左手系ですが、Vulkanでは右手系になっています。
たとえばMechtatelでは、以下のようにクリップ空間座標の$y$軸を反転する処理を行うことで、座標がVulkanで使用される右手系に一致するようにしています。
proj = new Matrix4f()
.scale(1.0f, -1.0f, 1.0f)
.perspective(cameraInfo.fovY, cameraInfo.aspect, zNear, zFar, true);正規化デバイス座標
gl_Positionにはクリップ空間座標がセットされており、その$x,y$成分は[-gl_Position.w, gl_Position.w]の値を取ります。
$z$成分は、OpenGLの場合[-gl_Position.w, gl_Position.w]、Vulkanの場合[0, gl_Position.w]の値を取ります。
正規化デバイス座標(Normalized Device Coordinates; NDC)はこれらの値を正規化したものになります。
具体的には、$x$成分と$y$成分は$[-1,1]$、$z$成分についてはOpenGLの場合$[-1,1]$、Vulkanの場合$[0,1]$とします。
先に示したように、gl_Positionの各成分を$w$成分で割ることで正規化することができます。
クリップ空間座標からNDCへの変換はOpenGLやVulkan側で自動的に行われるため、ユーザーが明示的に行う必要はありません。
クリップ空間座標をあらかじめ正規化しておけばいいのでは、と思われるかもしれません。
具体的には、たとえば頂点シェーダーで以下のような処理を明示的に行っておけばいいのでは、ということです。
gl_Position/=gl_Position.w;頂点シェーダーは各頂点について実行されますが、その後のフラグメントシェーダーは出力画像の各ピクセルについて実行されます。
頂点間にあるピクセルの色やNDCは各頂点の値から線形補間されます。
テクスチャ座標も各頂点の値から補間されますが、この補間は単純な線形補間ではなく、遠近法を考慮したものになっています。
テクスチャ座標の補間を行うために、ビュー空間での$z$座標の値が必要になるため、gl_Positionには正規化していないクリップ空間座標をセットする必要があるのです。
この補間処理については、このサイトで詳しく説明されています。
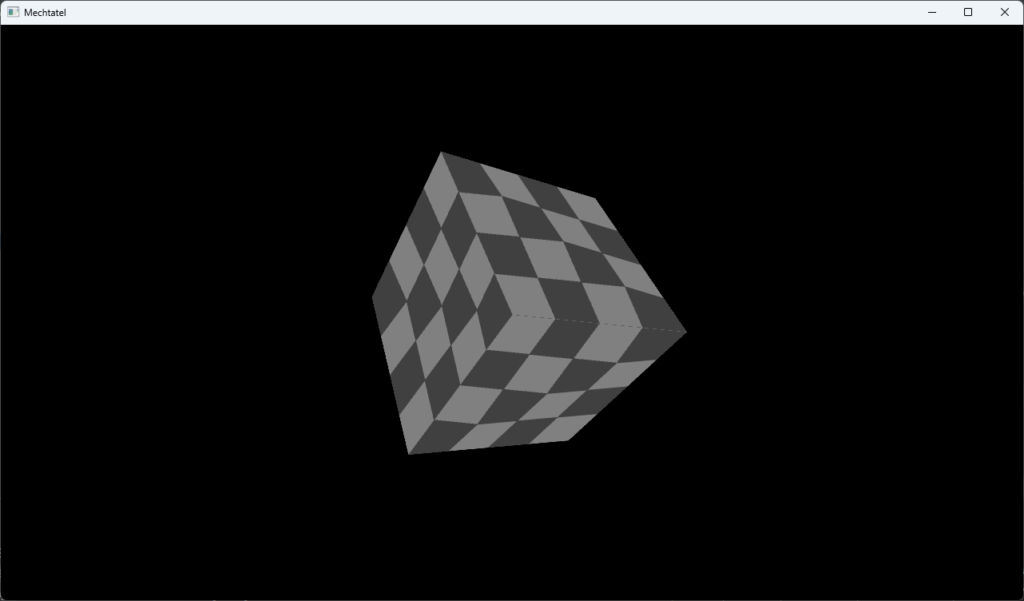
gl_Positionにあらかじめ正規化されたクリップ空間座標をセットした場合とそうでない場合の描画結果を以下に示します。gl_Positionをあらかじめ正規化している場合には、テクスチャ座標は単純に線形補間された値となり、見た目に歪みが生じているのがわかるかと思います。
gl_Positionをあらかじめ正規化した場合
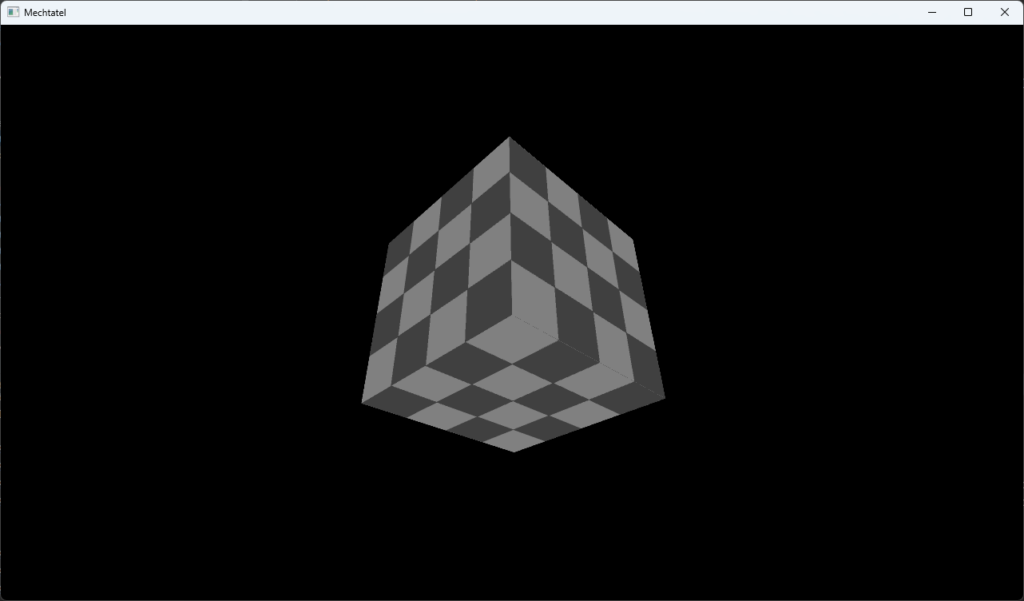
gl_Positionを正規化しない場合
スクリーン空間座標
スクリーン空間座標(screen-space coordinates)は描画結果を出力する画像、ひいては描画結果を表示するウィンドウの座標です。
NDCからスクリーン空間座標へのマッピング(ビューポート変換(viewport transformation))は自動的に行われます。
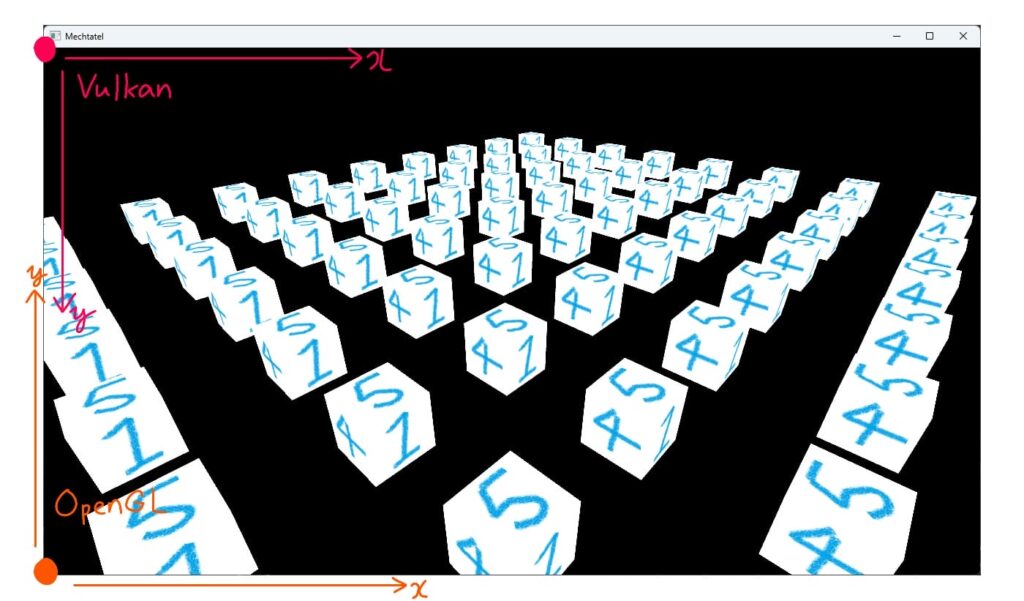
ビューポートの原点や大きさは、OpenGLならglViewport関数、VulkanならVkViewport構造体で設定します。
OpenGLではビューポートの左下を原点として右方向に$x$軸正の向き、上方向に$y$軸正の向きを取ります(左手系)。
一方Vulkanではビューポートの左上を原点として右方向に$x$軸正の向き、下方向に$y$軸正の向きを取ります(右手系)。
まとめ
かなり長い記事になってしまいましたが、頂点シェーダーで行っている座標変換の流れとしてはこんな感じです。
記事の内容に間違いなどありましたら、管理人まで連絡していただけるとありがたいです。