球の表面積を求める
まず、半径$r$の球について、極座標表示を用いて微小な表面積$dS$を求めます。
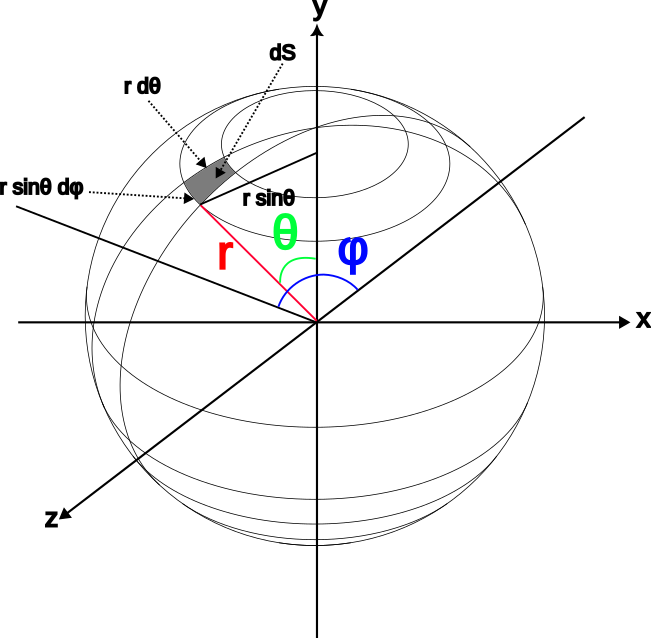
半径$r$の円周の長さは$2\pi r$で、このうち$\theta$ (rad)の弧の長さは
$$2\pi r\cdot\frac{\theta}{2\pi}=r\theta$$
このことより$dS$の$\theta$方向の長さは$rd\theta$、$\phi$方向の長さは$r\sin\theta d\phi$になるので、
$$
\begin{align}
dS&=rd\theta\cdot r\sin\theta d\phi \\
&=r^2\sin\theta d\theta d\phi
\end{align}
$$
となります。
$dS$を面積分すれば球の表面積が求められます。
$$
\begin{align}
\int_S dS&=\int_0^{2\pi}\left(\int_0^\pi r^2 \sin\theta d\theta \right) d\phi \\
&=r^2 \int_0^{2\pi}\left(\int_0^\pi \sin\theta d\theta \right) d\phi
\end{align}
$$
$$
\begin{align}
\int_0^\pi\sin\theta d\theta&=\left[ -\cos\theta \right]_0^\pi \\
&=-\cos\pi+\cos 0 \\
&=1+1 \\
&=2
\end{align}
$$
より、
$$
\begin{align}
\int_S dS&=r^2\int_0^{2\pi}\left(\int_0^\pi \sin\theta d\theta \right) d\phi \\
&=r^2\int_0^{2\pi}2d\phi \\
&=4\pi r^2
\end{align}
$$
したがって、半径$r$の球の表面積は$4\pi r^2$になります。