リーマンゼータ関数
導入
以下のように定義される$\zeta(s)$をリーマンゼータ関数(Riemann zeta function)と呼びます。
$$
\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}=1+\frac{1}{2^s}+\frac{1}{3^s}+\cdots\quad(\Re(s)>1)
$$
定義域
以前の記事でバーゼル問題を紹介しました。
バーゼル問題は$\zeta(2)$の値を求める問題ですね。
$s$が2より大きな実数の場合は$\frac{1}{n^s}$がより急速に小さくなっていくので、$\zeta(s)$が収束することは予想できると思います。
$\zeta(s)$が収束するかどうかの境界がどこにあるかというと、$s=1$にあります。
$s$を複素数とすれば、$\Re(s)>1$のとき$\zeta(s)$は収束します。
まずはこれを証明したいと思います。
$s=a+bi$とおくと、
$$
n^{-s}=n^{-a}n^{-ib}=n^{-a}e^{-ib\log n}
$$
なので、
$$
|n^{-s}|=n^{-a}
$$
です。
$n\le t\le n+1$において、$a>1$なら$n^{-a}>0$かつ$t^{-a}>0$なので、
$$
\begin{align}
&n^{-a}\ge t^{-a}\ge (n+1)^{-a} \\
&\Leftrightarrow \int_n^{n+1}n^{-a}dt\ge\int_n^{n+1}t^{-a}dt\ge\int_n^{n+1}(n+1)^{-a}dt \\
&\Leftrightarrow n^{-a}\ge\int_n^{n+1}t^{-a}dt\ge(n+1)^{-a}
\end{align}
$$
$n$について1から$N$までの和をとると、
$$
\int_1^{N+1}t^{-a}dt\ge -1^{-a}+\sum_{n=1}^{N+1}n^{-a}
$$
より、
$$
\begin{align}
\sum_{n=1}^{N+1}n^{-a}&\le 1+\int_1^{N+1}t^{-a}dt \\
&=1+\frac{1}{a-1}\left(1-(N+1)^{1-a}\right)
\end{align}
$$
$a>1$のとき、$0<(N+1)^{1-a}<1$、つまり$0<1-(N+1)^{1-a}<1$なので、
$$
\sum_{n=1}^{N+1}n^{-a}<1+\frac{1}{a-1}
$$
したがって、$a>1$のとき$\sum_{n=1}^{N+1}n^{-a}$は収束するので、$\zeta(s)$が$\Re(s)>1$で収束することがわかります。
積分表示
$\zeta(s)$の元の定義式だと$\Re(s)>1$の範囲でしか定義できませんが、解析接続によって定義域を$s\ne 1$の複素数にまで広げることができます。
その前段階として、まずは$\zeta(s)$の積分表示を導出します。
ガンマ関数$\Gamma(s)$
$$
\Gamma(s)=\int_0^\infty e^{-t}t^{s-1}dt
$$
で$t=nx$とおくと、
$$
\begin{align}
\Gamma(s)&=\int_0^\infty e^{-nx}(nx)^{s-1}\cdot ndx \\
&=\int_0^\infty n^se^{-nx}x^{s-1}dx \\
&=n^s\int_0^\infty e^{-nx}x^{s-1}dx
\end{align}
$$
なので、
$$
\frac{1}{n^s}=\frac{1}{\Gamma(s)}\int_0^\infty e^{-nx}x^{s-1}dx
$$
これより、$\zeta(s)$は、
$$
\begin{align}
\zeta(s)&=\sum_{n=1}^\infty\frac{1}{n^s} \\
&=\sum_{n=1}^\infty\frac{1}{\Gamma(s)}\int_0^\infty e^{-nx}x^{s-1}dx \\
&=\frac{1}{\Gamma(s)}\sum_{n=1}^\infty\int_0^\infty e^{-nx}x^{s-1}dx
\end{align}
$$
となります。
$$
\begin{align}
\sum_{n=1}^\infty e^{-nx}x^{s-1}&=x^{s-1}\sum_{n=1}^\infty e^{-nx} \\
&=x^{s-1}\lim_{n\to\infty}\frac{e^{-x}(1-e^{-xn})}{1-e^{-x}} \\
&=x^{s-1}\cdot\frac{e^{-x}}{1-e^{-x}} \\
&=\frac{x^{s-1}}{e^x-1}
\end{align}
$$
より、$\sum_{n=1}^\infty e^{-nx}x^{s-1}$は一様収束するので、積分と和の順番を入れ替えることができて、
$$
\begin{align}
\zeta(s)&=\frac{1}{\Gamma(s)}\int_0^\infty\left(\sum_{n=1}^\infty e^{-nx}x^{s-1} \right)dx \\
&=\frac{1}{\Gamma(s)}\int_0^\infty\frac{x^{s-1}}{e^x-1}dx
\end{align}
$$
と表すことができます。
積分表示(ハンケル積分路)
$$
\int_C\frac{(-z)^{s-1}}{e^z-1}dz
$$
を考えます。
積分路$C$は、以下に示すハンケル積分路(Hankel contour)です。
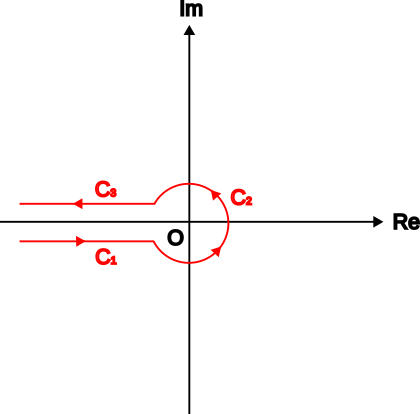
実軸の負の方向から原点に向かい、半径$\epsilon$の円弧を経由して再び実軸の負の方向に戻る積分路です。
上の図だと円弧の半径がそれなりに大きいように見えますが、実際には半径$\epsilon$は微小な値をとります。
まずは$C_1$の積分を計算します。
$-z=re^{-i\pi}$とおきます。
$$
\begin{align}
\int_{C_1}\frac{(-z)^{s-1}}{e^z-1}dz&=\int_\infty^0\frac{(re^{-i\pi})^{s-1}}{e^{-re^{-i\pi}}-1}\cdot (-e^{-i\pi})dr \\
&=\int_\infty^0\frac{r^{s-1}e^{-i\pi s}e^{i\pi}}{e^r-1}\cdot (-e^{-i\pi})dr \\
&=-\int_\infty^0\frac{r^{s-1}e^{-i\pi s}}{e^r-1}dr \\
&=-e^{-i\pi s}\int_\infty^0\frac{r^{s-1}}{e^r-1}dr \\
&=e^{-i\pi s}\int_0^\infty\frac{r^{s-1}}{e^r-1} \\
&=e^{-i\pi s}\Gamma(s)\zeta(s)
\end{align}
$$
同様にして$C_3$の積分も計算します。
$-z=re^{i\pi}$とおきます。
$$
\begin{align}
\int_{C_3}\frac{(-z)^{s-1}}{e^z-1}dz&=\int_0^\infty\frac{(re^{i\pi})^{s-1}}{e^{-re^{i\pi}}-1}\cdot (-e^{i\pi})dr \\
&=-\int_0^\infty\frac{r^{s-1}e^{i\pi s}e^{-i\pi}}{e^r-1}\cdot e^{i\pi}dr \\
&=-e^{i\pi s}\int_0^\infty\frac{r^{s-1}}{e^r-1}dr \\
&=-e^{i\pi s}\Gamma(s)\zeta(s)
\end{align}
$$
最後に$C_2$の積分を計算します。
$-z=\epsilon e^{i\theta}$とおいて、$\theta$を$-\pi$から$\pi$へ変化させます。
$$
\begin{align}
\left|\int_{C_2}\frac{(-z)^{s-1}}{e^z-1}dz\right|&=\left|\int_{-\pi}^\pi\frac{(\epsilon e^{i\theta})^{s-1}}{e^{-\epsilon e^{i\theta}}-1}\cdot (-i\epsilon e^{i\theta})d\theta\right| \\
&=\left|\int_{-\pi}^{\pi}\frac{\epsilon^{s-1}e^{i\theta s}e^{-i\theta}}{e^{-\epsilon e^{i\theta}}-1}\cdot (-i\epsilon e^{i\theta})d\theta\right| \\
&=\left|-i\epsilon^s\int_{-\pi}^{\pi}\frac{e^{i\theta s}}{e^{-\epsilon e^{i\theta}}-1}d\theta\right| \\
&=\epsilon^{\Re(s)}\left|\int_{-\pi}^\pi\frac{e^{i\theta s}}{e^{-\epsilon e^{i\theta}}-1}d\theta\right| \\
&\le\epsilon^{\Re(s)}\int_{-\pi}^\pi\left|e^{i\theta s}\right|\left|\frac{1}{e^{-\epsilon e^{i\theta}}-1}\right|d\theta \\
&=\epsilon^{\Re(s)}\int_{-\pi}^\pi\left|e^{i\theta s}\right|\left|\frac{1}{1-e^{-\epsilon e^{i\theta}}}\right|d\theta \\
&=\epsilon^{\Re(s)-1}\int_{-\pi}^\pi\left|e^{i\theta s}\right|\left|\frac{-\epsilon e^{i\theta}}{1-e^{-\epsilon e^{i\theta}}}\right|d\theta
\end{align}
$$
ロピタルの定理より、
$$
\lim_{z\to 0}\left|\frac{z}{1-e^z}\right|=\lim_{z\to 0}\left|\frac{1}{-e^z}\right|=1
$$
したがって、
$$
\lim_{\epsilon\to 0}\left|\frac{-\epsilon e^{i\theta}}{1-e^{-\epsilon e^{i\theta}}}\right|=1
$$
より、
$$
\int_{-\pi}^\pi\left|e^{i\theta s}\right|\left|\frac{-\epsilon e^{i\theta}}{1-e^{-\epsilon e^{i\theta}}}\right|d\theta
$$
は有界で、この値を$M$とすると、
$$
\left|\int_{C_2}\frac{(-z)^{s-1}}{e^z-1}dz\right|\le\epsilon^{\Re(s)-1}M\to0\quad(\epsilon\to0,\Re(s)>1)
$$
以上より、
$$
\begin{align}
\int_C\frac{(-z)^{s-1}}{e^z-1}dz&=e^{-i\pi s}\Gamma(s)\zeta(s)-e^{i\pi s}\Gamma(s)\zeta(s) \\
&=\left(e^{-i\pi s}-e^{i\pi s}\right)\Gamma(s)\zeta(s) \\
&=-2i\sin(\pi s)\Gamma(s)\zeta(s)
\end{align}
$$
$\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin(\pi s)}$より$\Gamma(s)\sin(\pi s)=\frac{\pi}{\Gamma(1-s)}$なので、
$$
\int_C\frac{(-z)^{s-1}}{e^z-1}dz=-\frac{2\pi i}{\Gamma(1-s)}\zeta(s)
$$
したがって、
$$
\zeta(s)=-\frac{\Gamma(1-s)}{2\pi i}\int_C\frac{(-z)^{s-1}}{e^z-1}dz\quad(\Re(s)>1)
$$
右辺の積分については、積分路$C$は被積分関数の極を通らないので、$s$の値によらず複素平面全体で正則です。
一方、$\Gamma(1-s)$は$s=1,2,3,\cdots$で極をもつので、これを除いた領域$D=\mathbb{C}\setminus\mathbb{N}\space(s\ne1,2,3,\cdots)$を考えます。
このとき、元の定義域を開集合$O=\{s\in\mathbb{C}\mid\Re(s)>1,s\notin\mathbb{N}\}$とすると、
- $O\subset D$
- $\zeta(s)$は$D$で正則
なので、一致の定理より、$\zeta(s)$は領域$D$でも成立します。
$$
\zeta(s)=
\left\{
\begin{aligned}
&\sum_{n=1}^\infty\frac{1}{n^s}\quad(\Re(s)>1) \\
&-\frac{\Gamma(1-s)}{2\pi i}\int_C\frac{(-z)^{s-1}}{e^z-1}dz\quad(s\ne 1,2,3,\cdots)
\end{aligned}
\right.
$$
の二つの式を合わせると、$\zeta(s)$を$s\ne 1$のすべての複素数$s$について定義することができます。
この後の計算の都合で$s$に制限をかけることがありますが、$\zeta(s)$自体は$s\ne 1$について定義できることを頭の片隅に置いておいてもらえるといいと思います。
自明な零点
$n$を自然数として$s=-n$とすると、
$$
\begin{align}
\zeta(-n)&=-\frac{\Gamma(1+n)}{2\pi i}\oint_C\frac{(-z)^{-n-1}}{e^z-1}dz \\
&=-\frac{n!}{2\pi i}\oint_C\frac{(-z)^{-n-2}}{e^z-1}\cdot (-z)dz \\
&=\frac{in!}{2\pi}\oint_C\frac{-z}{e^z-1}\cdot\frac{1}{(-z)^{n+2}}dz \\
&=\frac{in!}{2\pi}\oint_C\frac{-1}{(-1)^{n+2}z^{n+2}}\cdot\frac{z}{e^z-1}dz \\
&=\frac{in!}{2\pi}(-1)^{n+1}\oint_C\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1}dz
\end{align}
$$
留数定理より、
$$
\begin{align}
&\quad\frac{in!}{2\pi}(-1)^{n+1}\oint_C\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1}dz \\
&=\frac{in!}{2\pi}(-1)^{n+1}\cdot 2\pi i\mathrm{Res}\left(\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1},0\right) \\
&=-n!(-1)^{n+1}\mathrm{Res}\left(\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1},0\right) \\
&=n!(-1)^n\mathrm{Res}\left(\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1},0\right)
\end{align}
$$
ベルヌーイ数の定義より、
$$
\begin{align}
&\quad n!(-1)^n\mathrm{Res}\left(\frac{1}{z^{n+2}}\cdot\frac{z}{e^z-1},0\right) \\
&=n!(-1)^n\mathrm{Res}\left(\frac{1}{z^{n+2}}\sum_{k=0}^{\infty}\frac{B_k}{k!}z^k,0\right) \\
&=n!(-1)^n\mathrm{Res}\left(\sum_{k=0}^{\infty}\frac{B_k}{k!}z^{k-n-2},0\right)
\end{align}
$$
ローラン展開したときの-1次の係数が留数なので、$k-n-2=-1$より、
$$
\mathrm{Res}\left(\sum_{k=0}^{\infty}\frac{B_k}{k!}z^{k-n-2},0\right)=\frac{B_{n+1}}{(n+1)!}
$$
したがって、
$$
\zeta(-n)=n!(-1)^n\cdot\frac{B_{n+1}}{(n+1)!}=\frac{(-1)^n B_{n+1}}{n+1}
$$
$B_{n+1}$は$n$が偶数のときに0になるので、$\zeta(s)$は$s$が負の偶数のときに0になることがわかります。
これをリーマンゼータ関数の自明な零点(trivial zero)と呼びます。
相反公式
$\zeta(s)$と$\zeta(1-s)$の関係を表す相反公式(reflection formula)を導出します。
相反公式の導出のため、以下の積分を考えます。
$$
\int_{C_K}\frac{(-z)^{s-1}}{e^z-1}dz
$$
積分路$C_K$は以下のようなもので、鍵穴積分路(keyhole contour)と呼ばれることがあります。
ハンケル積分路の外側に、半径$R$の円弧を追加した積分路です。
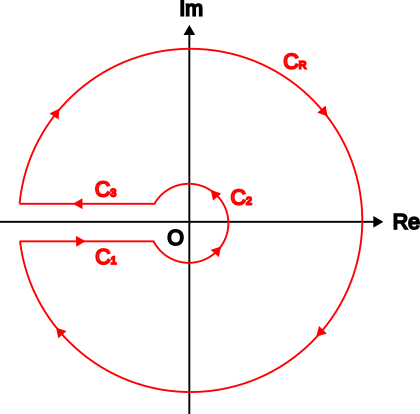
$s$を$s>1$の実数とします。
このとき、$\frac{(-z)^{s-1}}{e^z-1}$は$z=\pm 2n\pi i$ ($n$は自然数)で極をもちます。
$C_R$の半径$R$を$R=(2N+1)\pi$ ($N$は自然数)とすることでこの極を通らないようにできるので、今回はこの値を採用します。
ここでの計算の方針ですが、留数定理を用いた値と直接積分を計算した値を比較することで、相反公式を導出できます。
まずは留数定理を用いた計算です。
留数を求める際に極の位数が必要なので、まずはそれを求めます。
ある関数が$z=a$で$n$位の極をもつとき、分母に$(z-a)^n$という形が現れます。
これを$n$回微分すると$n!$になるので、$n$回微分の$z=a$での値が0でないことを確認すれば、極の位数が$n$であることがわかります。
今回の場合、$f(z)=e^z-1$とおくと、$f'(z)=e^z$です。
$f'(\pm 2n\pi i)=1\ne 0$より、極の位数は1となります。
留数定理より、
$$
-\frac{1}{2\pi i}\int_{C_R}\frac{(-z)^{s-1}}{e^z-1}dz=\sum_{n=1}^N\left(\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},2n\pi i\right)+\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},-2n\pi i\right)\right)
$$
左辺の符号がマイナスになっているのは、$C_R$の積分の向きが$C_2$の逆だからです。
$$
\begin{align}
\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},2n\pi i\right)&=\lim_{z\to 2n\pi i}(z-2n\pi i)\frac{(-z)^{s-1}}{e^z-1} \\
&=\lim_{z\to 2n\pi i}\frac{(-z)^{s-1}+(z-2n\pi i)(s-1)(-z)^{s-2}(-1)}{e^z} \\
&=(-2n\pi i)^{s-1} \\
&=(2n\pi)^{s-1}(-i)^{s-1} \\
&=\frac{(2n\pi)^{s-1}}{-i}(-i)^s \\
&=i(2n\pi)^{s-1}e^{-i\frac{\pi}{2}s}
\end{align}
$$
同様の計算で、
$$
\begin{align}
\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},-2n\pi i\right)&=\lim_{z\to 2n\pi i}(z+2n\pi i)\frac{(-z)^{s-1}}{e^z-1} \\
&=(2n\pi i)^{s-1} \\
&=(2n\pi)^{s-1}i^{s-1} \\
&=\frac{(2n\pi)^{s-1}}{i}i^s \\
&=-i(2n\pi)^{s-1}e^{i\frac{\pi}{2}s}
\end{align}
$$
となるので、
$$
\begin{align}
&\quad\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},2n\pi i\right)+\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},-2n\pi i\right) \\
&=i(2n\pi)^{s-1}e^{-i\frac{\pi}{2}s}-i(2n\pi)^{s-1}e^{i\frac{\pi}{2}s} \\
&=i(2n\pi)^{s-1}\left(e^{-i\frac{\pi}{2}s}-e^{i\frac{\pi}{2}s}\right) \\
&=i(2n\pi)^{s-1}\cdot\left(-2i\sin(\frac{\pi s}{2})\right) \\
&=2\cdot (2n\pi)^{s-1}\sin(\frac{\pi s}{2}) \\
&=2^s (n\pi)^{s-1}\sin(\frac{\pi s}2{})
\end{align}
$$
$$
\begin{align}
-\frac{1}{2\pi i}\int_{C_R}\frac{(-z)^{s-1}}{e^z-1}dz&=\sum_{n=1}^N\left(2^s(n\pi)^{s-1}\sin(\frac{\pi s}{2})\right) \\
&=2^s\pi^{s-1}\sin(\frac{\pi s}{2})\sum_{n=1}^N n^{s-1} \\
&=2^s\pi^{s-1}\sin(\frac{\pi s}{2})\sum_{n=1}^N\frac{1}{n^{1-s}}
\end{align}
$$
$N\to\infty$とすれば、
$$
-\frac{1}{2\pi i}\int_{C_R}\frac{(-z)^{s-1}}{e^z-1}dz=2^s\pi^{s-1}\sin(\frac{\pi s}{2})\zeta(1-s)
$$
となります。
$C_2$についても留数定理を用いて計算します。
$$
\begin{align}
\frac{1}{2\pi i}\int_{C_2}\frac{(-z)^{s-1}}{e^z-1}dz&=\mathrm{Res}\left(\frac{(-z)^{s-1}}{e^z-1},0\right) \\
&=\lim_{z\to 0}z\cdot\frac{(-z)^{s-1}}{e^z-1} \\
&=\lim_{z\to 0}\frac{(-1)^{s-1}z^s}{e^z-1} \\
&=\lim_{z\to 0}\frac{(-1)^{s-1}sz^{s-1}}{e^z} \\
&=0
\end{align}
$$
したがって、$C_K$全体では、
$$
\begin{align}
\frac{1}{2\pi i}\int_{C_K}&=\frac{1}{2\pi i}\int_{C_R}+\frac{1}{2\pi i}\int_{C_2} \\
&=-2^s\pi^{s-1}\sin(\frac{\pi s}{2})\zeta(1-s)
\end{align}
$$
となります。
留数定理を使わずに$\int_{C_K}$を求めます。
$C_R$以外はすでに求めてあるので、$\int_{C_K}=\int_C+\int_{C_R}$で計算できます。
$-z=Re^{i\theta}$とおいて、$\theta$を$\pi$から$-\pi$へ変化させます。
$$
\begin{align}
\left|\int_{C_R}\frac{(-z)^{s-1}}{e^z-1}dz\right|&=\left|\int_\pi^{-\pi}\frac{\left(Re^{i\theta}\right)^{s-1}}{e^{-iRe^{i\theta}}-1}\cdot(-iRe^{i\theta})d\theta\right| \\
&=\left|\int_\pi^{-\pi}\frac{R^{s-1}e^{i\theta s}e^{-i\theta}}{e^{-iRe^{i\theta}}-1}\cdot(-iRe^{i\theta})d\theta\right| \\
&=\left|-iR^s\int_\pi^{-\pi}\frac{e^{i\theta s}}{e^{-iRe^{i\theta}}-1}d\theta\right| \\
&=R^{\Re(s)}\left|\int_\pi^{-\pi}\frac{e^{i\theta s}}{e^{-iRe^{i\theta}}-1}d\theta\right| \\
&\le R^{\Re(s)}\int_\pi^{-\pi}\left|e^{i\theta s}\right|\left|\frac{1}{e^{-iRe^{i\theta}}-1}\right|d\theta
\end{align}
$$
$$
\lim_{R\to\infty}\left|\frac{1}{e^{-iRe^{i\theta}}-1}\right|=1
$$
より、
$$
\int_\pi^{-\pi}\left|e^{i\theta s}\right|\left|\frac{1}{e^{-iRe^{i\theta}}-1}\right|d\theta
$$
は有界で、この値を$M$とおくと、
$$
\left|\int_{C_R}\frac{(-z)^{s-1}}{e^z-1}dz\right|\le R^{\Re(s)}M\to 0\quad(R\to\infty,\Re(s)<0)
$$
となります。
したがって、
$$
\int_{C_K}=\int_C+\int_{C_R}=\int_C=-\frac{2\pi i}{\Gamma(1-s)}\zeta(s)
$$
留数定理を用いて計算した値と直接計算した値を比較します。
留数定理を用いて計算した値
$$
\frac{1}{2\pi i}\int_{C_K}\frac{(-z)^{s-1}}{e^z-1}dz=-2^s\pi^{s-1}\sin(\frac{\pi s}{2})\zeta(1-s)
$$
直接計算した値
$$
\frac{1}{2\pi i}\int_{C_K}\frac{(-z)^{s-1}}{e^z-1}dz=\frac{1}{2\pi i}\left(-\frac{2\pi i}{\Gamma(1-s)}\zeta(s)\right)=-\frac{\zeta(s)}{\Gamma(1-s)}
$$
したがって、
$$
-2^s\pi^{s-1}\sin(\frac{\pi s }{2})\zeta(1-s)=-\frac{\zeta(s)}{\Gamma(1-s)}
$$
より、
$$
\zeta(s)=2^s\pi^{s-1}\sin(\frac{\pi s}{2})\Gamma(1-s)\zeta(1-s)
$$
$s=-2n$ ($n$は自然数)をこの式に代入すると
$$
\zeta(-2n)=2^{-2n}\pi^{-2n-1}\sin(-\pi n)\Gamma(1+2n)\zeta(1+2n)
$$
となることからも、$s$が負の偶数のときに$\zeta(s)=0$となることがわかります。