光円錐
世界間隔の二乗を$ds^2=-(cdt)^2+dx^2+dy^2+dz^2$と表すことを前回紹介しました。
今、ある地点から光を発することを考えます。
このとき、その光の経路上では、$\sqrt{dx^2+dy^2+dz^2}=cdt$が成立します。
光の進んだ空間上の距離(左辺)が光速度×時間で表される距離(右辺)に等しくなる、という関係式です。
このことより、光の経路上では$ds^2=-(cdt)^2+dx^2+dy^2+dz^2=0$が成立します。
この式で定義される4次元空間中の円錐を光円錐(light cone)と呼びます。
$y=0$として次元を3に下げた図を以下に示します。
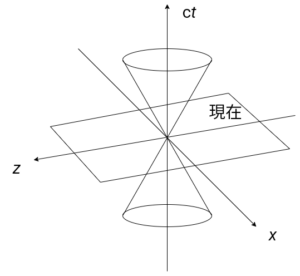
光よりも遅い粒子の経路上では$ds^2<0$、光より速い運動の経路上では$ds^2>0$となります。
$ds^2<0$の場合その経路は時間的(time-like)、$ds^2=0$の場合は光的(light-like)、$ds^2>0$の場合は空間的(space-like)と言います。